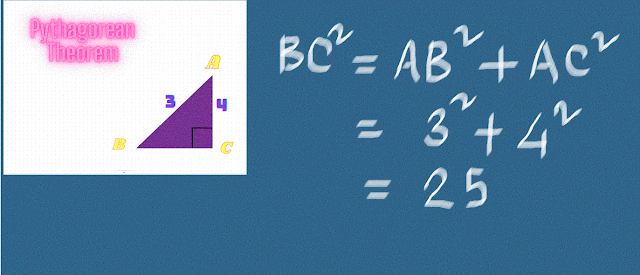Square Roots: Pythagoras
Geometry
The square on the hypotenuse of a right-angled triangle is equal to the sum of the squares on the other two sides.
The square of a number is that number times itself. A square is expressed as, for example, 6 square, which means 6 x 6, or 6 squared. The square root of a number is the value that, multiplied by itself, equals that number. The square root of 36 is 6. This is expressed as √36 = 6.
Not all square roots of numbers are whole numbers, like 6. Numbers that have a whole number as their square root are called perfect squares.
Suppose we draw two intersecting lines, AB and AC at right angles to each other. If AB = 3 units and AC = 4 units, the triangle ABC is determined and the length of BC is fixed. So the length of AB (called the hypotenuse of the right-angled triangle ABC) must depend on the lengths of the other two sides.
Q. What is the relation which connects the lengths of the three sides of a right-angled triangle?
The relation, first proved rigorously by Pythagoras, a Greek philosopher and geometrician, was known in practice long before his time. It was, in fact, used by the ancient Egyptians for the construction of right angles.
The theorem states that the square on the hypotenuse of a right-angled triangle is equal to the sum of the squares on the other two sides.
The hypotenuse BC is therefore 5 units long.
Ex.1. In the triangle, ABC, AC = 4.2 cm and BC = 3.4 cm and angle C is a right angle. Find the length of AB.
AB² = AC² + BC² (Pythagoras)
= 4.2² + 3.4²
= 17.64 + 11.56
= 29.2 cm²
AB = 5.4 cm
Ex. 2. In the triangle ABC, AD is the perpendicular from A to BC. Given that AB = 13 cm, AD = 12 cm and AC = 15 cm, find the length of BC.
AD² + BD² = AB² (Pythagoras)
12² + BD² = AB²
BD² = 13² - 12²
= 25
BD = 5 cm
Also AD² + DC² = 15²
DC² = 15² - 12²
= 81
DC = 9 cm
The length of BC is 5 cm + 9 cm or 14 cm.
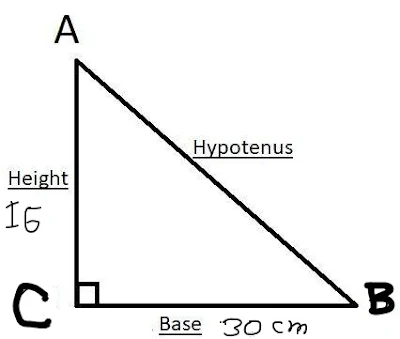
Q.3. ABC which is right-angled at C.Given AC= 16 cm, BC = 30 cm find AB.
We are given, AC = 16 cm, BC = 30 cmAB² = AC² + BC² = (16)² + (30)² = 1156 = √1156AB = 34
Rational Numbers as Fractions:
A number that can be written as the ratio of two integers is called a rational number. For example, the fraction 1/3 is a rational number because it is the ratio 1 to 3. The number 2 is a rational number because it can be written as 2/1, or the ratio of 2 to 1. A decimal is also a rational number because it can be written as a fraction, For example, 0.234 = 234/1000.
A fraction whose numerator is greater than its denominator is called an improper fraction. An improper fraction can be changed to a mixed numeral, a number written as a whole number and a fraction. To change an improper fraction to a mixed numeral, divide the numerator by the denominator. For example,
18/7 means 18 divide by 7. Because 7 divides into 18 two times with a remainder of 4, 18/7 equals 2 4/7.
To change a mixed numeral into an improper fraction, multiply the whole number by the denominator and add the numerator. Place this number over the denominator.
Understanding Rational and Irrational Numbers:
A rational number is a number that either terminates or repeats a pattern. It can be written as a fraction, a/b, where a and b are both whole number integers and b does not equal zero.
Her are some examples of rational numbers: 3, -5, 1/3, 4.66, 5/11, 3.25
An irrational number is any decimal that does not terminates and never repeats. These numbers are often represented by symbols.
Her are some examples of irrational numbers: 5.23143........,√5, π
Not all square roots of numbers are whole numbers, like 6. Numbers that have a whole number as their square root are called perfect squares.
the cube root of 27 is 3. ∛27 = 3, because 3 x 3 x 3 = 27. Numbers that have a whole number cube root are called perfect cubes.
The square root or cube root of any number that is not a perfect square is called a radical number. the symbols √ and ∛ are called radical signs. When a number is not perfect square, you can estimate its square toot by determining which perfect squares it comes between.
√50 is a little more than 7, because √49 is exactly 7. √60 is between 7 and 8 but is closer to 8, because 60 is closer to 64 than to 49. The same strategy can be used for cube roots.
Comparing Rational & Irrational Numbers:
Compare rational and irrational numbers by using a best guess for irrational numbers.
√3 <2 This statement is true because √3 is between 1 and 2.
5>√20 this statement is true because √20 is between 4 and 5.
Approximate the value of an irrational number by exploring values.
The value of √2 is between 1 and 2. Look at the squares of 1.4 and 1.5.
1.4² = 1.96
1.5² = 2.25
by looking at these squares, it is evident that √2 is between 1.4 and 1.5.
Rational and irrational numbers can be compared by approximating their value and placing them along a number line, such as the numbers √5, 2.5, √3
Solving Equations with rational numbers:
To solve an equation with rational numbers, you must find a value that makes the variable in the equation true. To do this, use inverse operations to rearrange the equation so that the variable is alone on one side. Inverse operations are operations that have the opposite effect, like addition and subtraction or multiplication and division. Remember that whatever you do to one side of the equation, you must also do to the other side of the equation.
Ex. a + 2.4 = 6.5