Algebric Expression:
An algebraic expression is a mathematical phrase that can include numbers, variables (letters that represent unknown values), and operation symbols (such as +, -, ×, ÷). Unlike an equation, an algebraic expression does not have an equal sign.
The word algebra comes from an Arabic word (al-jabr, literally means restoration). Its roots can be traced to a mathematician, Muhammed bin Musa al-Khwarizmi (780 - 850).
He wrote the Compendious Book on Calculation by Compendious Book on Calculation by Completion and Balancing, which established algebra as a mathematical discipline that is independent of geometry and arithmetic.
Q. What is algebraic expressions?
Ans: Meaningful organization of operational signs and numerical letter symbols is called Algebraic Expressions.
Such as, 2a + 3b - 4c is an algebraic expressions.In algebraic expression, different types of information are expressed through the letters a,b,c,p,q, m,n,x,y,z.........etc.These alphabet are used to solve different types of problems related to algebraic expressions.
In arithmetic, only positive numbers are used, where as, in algebra, both positive and negative numbers including 0 are used.Algebra is the generalization of arithmetic.The numbers used in algebraic expressions are constants, their values are fixed.The letter symbol used in algebraic expressions are constants, their values are fixed.The letter symbol used in algebraic expressions are variables, their values are not fixed, they can be of any value.
Q. What is algebraic formula?
Ans: Any general rule or resolution expressed by algebraic symbols is celled Algebraic formula.Formula:(a+b)² = a² + 2ab + b²(a - b)² = a² - 2ab + b²
Corollary:
1. a² + b² =(a + b)² ─ 2ab
2. a² + b² =(a- b)² + 2ab
3. (a + b)² =(aーb)² + 4ab
4. (a ─ b)² =(a + b)² - 4ab
5. a² - b² = (a + b) (a- b)
Formula-4:
(x + a) (x + b) = x² + ( a +b ) x + ab
Formula-5:
(a + b +c)² = a² + b² + c² + 2ab + 2bc + 2ac
Corollary - 7:
a² + b² + c² = (a + b +c)² - 2( ab +bc + ca)
Corollary - 8:
2(ab + bc + ac ) = (a + b +c) ² - ( a² + b² + c²)
Ex.1. What is the square of (4x + 5y) ?
Solution:
( 4x + 5y) = (4x )² + 2. (4x) . (5y) + (5y)²
= 16x² + 40 xy + 25 y²
Ex.2. What is the square of (3a - 7b) ?
(3a - 7b)²
= (3a) - 2.3a.7b + (7b)²
= 9a² - 42ab + 49b²
Ex. 3. Find the square of 996 by applying the formula of square.
(996) = (1000 - 4)
= (1000)² - 2.1000.4 + 4²
= 992016
4. What is the square of a+b+c+d?
(a + b + c + d)²
= { (a + b) + ( c + d) }²
= ( a + b)² + 2 ( a + b) (c + d) + ( c + d)²
= (a + b)² + 2 ( a +b) (c + d) + ( c + d)²
= a² + 2ab + b² + 2(ac + ad + bc + bd) + c² + 2cd + d²
= a² + 2ab + b² + 2ac + 2ad +2bc +2bd + c² + 2cd + d²
Ex.5. Simplify:
(5x + 7y + 3z)² + 2 (7x - 7y - 3z) (5x + 7y + 3z) + ( 7x - 7y - 3z)²
Let, 5x + 7y + 3z = a
5x + 7y + 3z = b
Given expression = a² + 2ab + b²
= (a + b)²
= (5x + 7y + 3z + 7x - 7y - 3z)²
Substituting the value of a and b
= (12x)²
= 144x² Ans.
Ex.6. If x - y = 2 and xy = 24,
What is the value of x + y?
Solution:
(x + y)² = (x - y)² + 4xy
= 2² + 4 x 24
= 100 Ans.
Ex. 7. If a⁴ + a²b² + b⁴ = 3
a² + ab + b² = 3
What is the value of a² + b² ?
Solution:
a⁴ + a²b² + b⁴
= (a²)² + 2a²b² + (b²)² - a²b²
= (a² + b²) - (ab)²
= (a² + ab + b²) ( a² - ab + b²)
∴ = 3 = 3 (a² - ab + b² )
( Substituting the values)
or a² - ab + b² = 3/3 = 1
Now adding , a² + ab + b² = 3
a² - ab + b² = 1
We get, 2 (a² + b²) = 4
or, a² + b² = 2
∴ a² + b² = 2
Expressions and Variables:
A variable is a symbol, usually a letter of the alphabet, that stands for an unknown number, or quantity.
a = variable
An algebraic expression is a combination of numbers, variables, and at least one operation.
X + 13
An expression is a number phrase without an equals sign.
An algebraic expression is a number, variable, or combination of numbers and variables, connected by a mathematical operation like addition, subtraction, multiplication, or division. For example, in the expression X + 5, X is the variable.
A numerical expression contains only numbers: 3 + 6
A variable expression contains numbers and variables: 3 + b
All expressions express an idea.
5n means "five times n" or "five ns."
b - 3 means "b decreased by 3" or "a number decreased by 3."
In the expression 5n, both 5 and n are factors.
Equations & Inequalities:
A term is a number, variable, product, or quotient in an algebraic expression. In 3a + 5, 3a is a term and 5 also is a term.
The term 3a means 3 X a. The number 3 is the coefficient of a. A coefficient is a number that multiplies a variable. In the expression x + 5, the coefficient of x is understood to be 1.
An equation is a mathematical sentence that states that two expressions are equal. It contains an equals sign.
2 + 5 = 7
An inequality is a mathematical sentence that states that two expressions are not equal. It shows how two numbers or expressions compare to one another.
2 + 5> 6
2 + 5 < 9
Like expressions, equations and inequalities may contain only numerals, or they may also contain variables.
2 + c = 7
Long Division in Algebra
The degree of an expression in x is the degree of the highest power of x it contains
the degree of 2x³ - 4x² + 6x - 1 is 3.
When the expression is arranged so that the highest power of x comes first, the next highest power of x second and so on, it is said to be in descending powers of x.
When the powers of x increase, the expression is said to be arranged in ascending powers of x.
Ex. Divide 2x² + 7x + 6 by x + 2.
2x + 3
x + 2) 2x² + 7x + 6 (
2x² + 4x
__________
3x + 6
3x + 6
________
The quotient is 2x + 3.
Ex. 2 . Divide 4x⁴ - 3x³ + 2x² - 5x + 6 by x² - 3x - 1.
4x² - 9x - 33
x² - 3x - 1 ) 4x⁴ - 3x³ + 2x² - 5x + 6 (
4x⁴ - 12x³ + 4x²
__________________
9 x³ + 6x² - 5x
9 x³ + 27x² - 9x
____________________
33x² - 4x + 6
33x² - 99x-33
____________________
103 x + 39
The quotient is 4x² - 9x - 33;
The remainder is 103 x + 39.
Solving Linear Equations:
Finding an Unknown in a Formula:
a) V = ibh
When l = 5, b = 2, h = 3,
V = 5 x 2 x 3,
V = 30 cm³
Volume of the cuboid = 30 cm³
b) V = lbh
When V = 240, b = 6, h = 5,
l x 6 x 5 = 240
30l = 240
l = 240/30
= 8 cm
Length of the cuboid = 8 cm
Ex. If y + b = ay + c/b calculate the value of c when y = 12,
b = 3 and a = 14.
Solution:
y + b = ay + c/b
When y = 12, b=3, a = 14,
12 + 3 = 14 x 12 + c/3
15 = 168 + c/3
3 x 15 = 168 + c / 3
45 = 168 + c
45 - 168 = c
c = 123
Construction of a Formula
Ex. i) Find a formula for the sum S of any three consecutive even numbers.Solution:
Let the smallest even number be n.
The next even number will be n + 2.
The greatest even number will be (n + 2) + 2 = n + 4
S = n + (n + 2 ) + (n + 4)
= n + n + n + 2 + 4
= 3n + 6
ii) Hence, calculate the value of S when the smallest even number is 14.
Solution:
When the smallest even number is 14, i.e. n = 14
S = 3 x 14 + 6
= 48
Formulating an Equation:
Michael walks at an average speed of 3 km/h for 45 minutes before running for half an hour at a certain average speed. If he travels a total distance of 6 km, calculate his average running speed.
Solution:
Let Michael's average running speed be x km/h.
45 minutes = 45/60 hour = 3/4 hour
Total distance he walks = 3 x 3/4 = 9/4 km
Total distance he runs = x x 1/2 = x/2 km
9/4 + x/2 = 6
9/4 + 2x/4 = 6 (convert to like fractions: x/2 = 2x/4)
9 + 2x/4 = 6 ( combine into a single fraction)
9 + 2x = 6 x 4
9 + 2x = 24
2x = 15
x = 15/2
x = 7 1/2
Michael's average running speed is 7 1/2 km/h.
Solution:
* A formula expresses a rule in algebraic terms. It makes use of variables to write instructions for performing a calculation.
* To solve an inequality, we
Spectrum 7th Grade Math Workbooks, Ages 12 to 13, 7th Grade Math, Algebra, Probability, Statistics, Ratios, Positive and Negative Integers, and Geometry Workbook - 160 Pages (Volume 8) Paperback –
Support your child’s educational journey with the Spectrum grade 7 math workbook that teaches essential math skills to seventh graders.
Spectrum’s 7th grade math workbook is a great way for seventh graders to learn essential math skills such as learning algebra equations, geometry, positive and negative integers, and more through a variety of problem-solving activities that are both fun AND educational!
Why You’ll Love This Math Book
- Engaging and educational math for 7th graders. “evaluating algebraic expressions”, “solving word problems”, and “number line practice” are a few of the fun activities that incorporate math in everyday settings to help inspire learning.
- Testing progress along the way. Pretests, posttests, a mid-test, final test, and an answer key are included in the 7th grade math workbook to help track your child’s progress along the way before moving on to new and exciting math lessons.
- Practically sized for every activity The 160-page math workbook is sized at about 8.5 inches x 10.75 inches—giving your child plenty of space to complete each exercise.
About Spectrum
For more than 20 years, Spectrum has provided solutions for parents who want to help their children get ahead, and for teachers who want their students to meet and exceed set learning goals—providing workbooks that are a great resource for both homeschooling and classroom curriculum.
The Spectrum Grade 7 Math Workbook Contains:
- 7 chapters full of vibrant activities and illustrations
- Pretests, posttests, mid-test, final test, scoring record, and answer key
- Perfectly sized at about 8.5" x 10.75"
Click here!
Problem solving with linear Models
- Identify and interpret the intercept of a linear model.
- Calculate and interpret the slope of a linear model.
- State the equation of the line in slope-intercept form.
Intercept:
The point where the line intersects the y-axis
Slope:
The ratio of change in y to change in x between two points in a line.
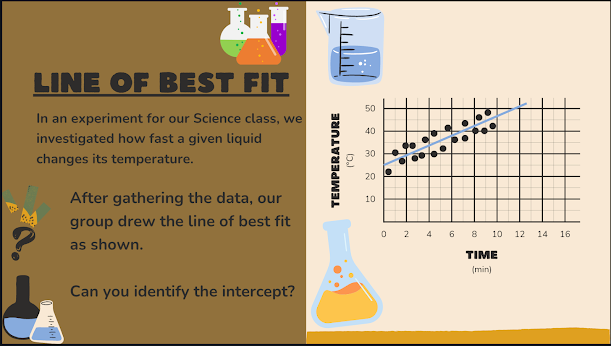
A set of data may be scattered as the one shown in the graph but can be represented by a line of best fit.
A straight line that best represents a set of scattered data.
n an experiment for our Science class, we investigated how fast a given liquid changes its temperature.
After gathering the data, our group drew the line of best fit as shown.
Can you identify the intercept?
Recall that the y-intercept refers to the point where the line intersects the y-axis.
Identifying the Intercept of the Line
Looking at the graph, the line intersects the y-axis at 25.
The y-intercept is thus 25.
Interpreting the Intercept of the Line
What information can the y-intercept tell us?
The y-intercept is also the value of y when x = 0.
Looking at the graph again, we can then say that the temperature of the liquid before heating (time = 0), is 25°C.
Slope is the ratio of the change in y and the change in x.
This can be calculated using two points on the line with the formula:
This slope tells us that the temperature increases by 2.5°C every minute.
Using the y-intercept (b) and the slope (m), the line of best fit may be represented through an equation.