Area & Perimeter of Trapezium
* A quadrilateral having one pair of parallel sides is called a trapezium.
* A figure surrounded by 4 straight lines is called a quadrilateral.
* A line segment joining two opposite pairs of vertices is called a diagonal. A quadrilateral has two diagonals, but a triangle does not have any diagonal.
* A trapezium is a quadrilateral in which one pair of opposite sides are parallel to each other.
In trapezium ABCD, AB॥DC but BC∦AD.
A trapezium is not a quadrilateral.
Area of a trapezium
= 1/2 x (sum of lengths of parallel sides ) x height
= 1/2 (a + b) h* A quadrilateral with one pair of sides parallel is called a trapezium.
Suppose that AB = a and DC = b and that the distance between AB and CD is h.
The area of triangle ABD is 1/2ah.
The area of triangle DCB is 1/2bh.
The area of ABCD is
1/2ah + 1/2bh = 1/2(a + b)h.
So the area of a trapezium is equal to one-half the product of the sum of the parallel sides and the distance between them.
Ex. 18
7. ABCD is a trapezium with AB parallel to DC. If the angles A and B are equal, prove that the angles C and D must be equal.
We are given that ABCD is the trapezium and AB parallel to DC.
We are also given that angle A and angle B are equal to angle D.
Q.1. Finding Area and Perimeter of a Trapezium)
The figure shows a trapezium ABCD where
AB = 12.9 cm,
BC = 8 cm
CD = 4 cm
AD = 7 cm.
If DE = 6 cm, calculate
i) the area
ii) the perimeter of the trapezium
Solution:
Area of the trapezium
= ½ x (sum of lengths of parallel sides ) x height
= ½ x ( 12.9 + 4 ) x 6
= 50.7 cm2
ii) Perimeter of the trapezium = AB + BC + DC + AD
= 12.9 + 8 + 4 + 7
= 31.9 cm
New Syllabus
Mathematics 7th Edition
Ex. - 13B
Basic Level:
1. Complete the table for each parallelogram:
Base ----- Height ------- Area
a) 12 cm ------- 7 cm --------- ?
b) ? -- ---- 6cm ------ 42 m²
c) 7.8 mm ---- ? ------ 42.9 mm²
a) Given here,
base = 12 cm
height = 7cm
Area = ?
We know that,
Area of the parallelogram = base X height
= 12 X 7
= 84 cm²
b) a) Given here,
base = ?
height = 6 cm
Area = 42 m²
We know that,
Area of the parallelogram = base X height
42 = base X 6 cm
base = 42/6
= 7 cm Ans.
c) a) Given here,
base = 7.8 mm
height = ?
Area = 42.9 mm²
We know that,
Area of the parallelogram = base X height
42.9 mm² = 7.8 mm X height
height = 42.9/ 7.8
= 5.5 m Ans.
2. Complete the table for each trapezium.
Parallel side 1 ---- Parallel side 2 ----- height ---- Area
a) 7 cm -------- 11 cm ------ 6 cm ---- ?
b) 8m ----- 10 m ------- ? ---- 126 m²
c) 5 mm ----- ? ------- 8 mm ---- 72 mm²
a) Given here,
Parallel side 1 = 7 cm
Parallel side 2 = 11 cm
height = 6 cm
Area = ?
We know that,
Area of the trapezium = 1/2 X ( sum of lengths of parallel sides) X height
= 1/2 X ( 7 + 11) X 6
= 1/2 X 18 X 6
= 54 cm²
b) Given here,
Parallel side 1 = 8 cm
Parallel side 2 = 10 cm
height = ?
Area = 126 m²
We know that,
Area of the trapezium = 1/2 X ( sum of lengths of parallel sides) X height
126 m² = 1/2 X (8 + 10 ) X height
126 m² = 1/2 X 18 X height
height = 126/9
height = 14 m Ans.
c) Given here,
Parallel side 1 = 5 cm
Parallel side 2 = PQ
height = 8 mm
Area = 72 mm²
We know that,
Area of the trapezium = 1/2 X ( sum of lengths of parallel sides) X height
72 mm² = 1/2 X ( 5mm + PQ) X 8 mm
72 mm² = 4 X (5 mm + PQ)
(5mm + PQ) = 18
PQ = 13 mm Ans.
3. The figure shows a parallelogram ABCD where AB = 10cm and BC = 6 cm. If DE = 9cm, find
i) the area,
ii ) the perimeter,
of the parallelogram.
Solution:
Given here,
base = 6 cm
height = 9 cm
Area = ?
We know that,
Area of the parallelogram = base X height
= 6 X 9
= 54 cm²
Perimeter of the parallelogram = 10 X 2 + 6 X 2
= 32 cm
4. The figure shows a parallelogram PQRS where QR = 10m. If ST = 8 m and SU = 11.2m, find the length of PQ.
PQ X ST = PS X SU
PQ X 8 = 10m X 11.2m
PQ = 14 m Ans.
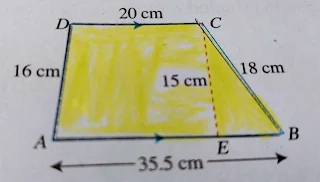
5. The figure shows a trapezium ABCD where AB = 35.5 cm, BC = 18 cm, CD = 20 cm and AD = 16 cm, If CE = 15 cm, find
i) the area,
ii) the perimeter,
of the trapezium.
Solution:
i) Given here,
Parallel side 1 = 35.5 cm
Parallel side 2 = 20 cm
height = 15 cm
Area = ?
We know that,
Area of the trapezium = 1/2 X ( sum of lengths of parallel sides) X height
= 1/2 X ( 35.5cm + 20cm ) X 15 cm
= 1/2 X 55.5 cm X 15 cm
= 416.25
ii) Perimeter of the trapezium = AB + BC + CD + AD
= 35.5 cm + 18cm + 20 cm + 16 cm
= 89.5 cm Ans.
6. The figure shows a trapezium PQRS where PQ = 12 m and PS = 13 m. If PT = 10 m, and the area and the perimeter of the trapezium are 150 m² and 54.7 m respectively, find the length of
i) RS,
ii) QR.
i) We know that,
Area of the trapezium = 1/2 X ( sum of lengths of parallel sides) X height
150 m² = 1/2 X ( PQ + RS) X 10 m
150 m² = 1/2 X ( 12 + RS) X 10 m
RS = 18 m Ans.
ii) Perimeter of the trapezium = PQ + QR + RS + PS
54.7 m = 12 + QR + 18m + 13m
54.7 m = QR + 43
QR = 11.7 m Ans.
7. The figure shows a trapezium ABCD where AB is perpendicular to AD, AB = 12 cm, BC = 14 cm and AD = 10 cm. Find the area of the shaded regions.