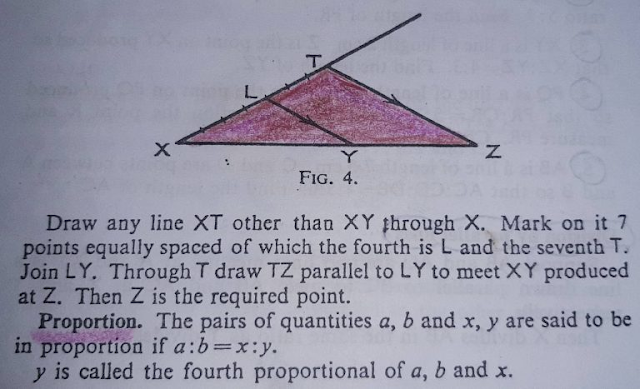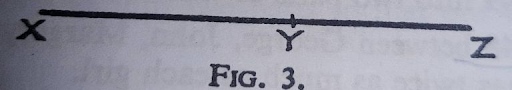Pythagorean Theorem
One of the most famous theorems in mathematics is the Pythagorean Theorem, named for the Ancient Greek mathematician Pythagoras. This theorem can be used to find information about the lengths of the sides of a right triangle.
Real Life Applications:
- Building and architecture
- Navigation and GPS
- Games and sports
What other examples can you think of for using the Pythagorean Theorem in your life?
Q. Who discovered this theorem?
Pythagoras was an ancient Greek philosopher and mathematician, born around 570 BCE on the island of Samos in the eastern Aegean Sea. Pythagoras founded a religious and philosophical school in Croton (now Crotone) in southern Italy, known as the Pythagorean school. Pythagoras and his followers made significant contributions to mathematics, including discoveries in geometry, arithmetic, and number theory.
The ancient Greek mathematician and philosopher Pythagoras is credited with discovering this relationship in the 6th century BCE due to the prominence of his religious-mathematical school in Croton, Italy.
The Pythagorean Theorem has been proved through hundred of methods and new proofs are still being discovered.
Here is an example of a visual proof showing the squares of the sides.
Notice, 9 + 16 = 25!
- The Pythagorean Theorem states that, in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs.
- Identify the two legs of the triangle and the hypotenuse.
- Note their lengths.
- Determine which side you are trying to find.
- Substitute your lengths into the Pythagorean Theorem equation and solve for the missing value.
- A right angle creates many special relationships between the sides and angles of the triangle and is the basis of the mathematical branch of trigonometry.
1. What is a theorem?
Ans: A theorem is a statement in mathematics or logic that can be proved to be true by reasoning. The proof of a theorem is a logical argument that uses the inference rules of a deductive system to establish that the theorem is a logical consequence of the axioms, and previously proved theorems.
2. Why are Theorems Important in Maths?
Ans: Theorems not only form the foundation of basic mathematics but also help them to develop deductive reasoning when they completely understand the statements and their proofs.
Theorems are of significance and are considered as absolute truths. They not only help to solve mathematical problems easily but their proofs also help to develop a deeper understanding of the underlying concepts. For students, theorems are not only from the foundation of basic mathematics but also help them to develop deductive reasoning when they completely understand the statements and their proofs.
A theorem is a statement that can be demonstrated to be true by accepted mathematical operations and arguments. In mathematics, a theorem is a statement that has been proved or can be proved.
Since the time of the ancient Greeks, proven theorems have represented the foundation of mathematics.
Perhaps the most famous of all theorems is the Pythagorean theorem,
which was created by the Greek mathematician and philosopher Pythagoras of Samos (c. 582–c. 507 BC).
KEY TERMS
Axiom —A basic statement of fact that is stipulated as true without being subject to proof.
Deductive reasoning — A type of logical reasoning that leads to conclusions which are undeniably true if the beginning assumptions are true.
Pythagorean theorem — An idea suggesting that the sum of the squares of the sides of a right triangle is equal to the square of the hypotenuse. It is used to find the distance between two points.
List of Theorems:
1. A straight line drawn parallel to one side of a triangle divides the other sides in the same ratio
2. If a straight line divides two sides of a triangle in the same ratio, then the line is parallel to the other side of the triangle
3. If two triangles are equiangular their corresponding sides are proportional
4. If two triangles have their corresponding sides proportional, they are equiangular
5. If two triangles have one angle of the one equal to one angle of the other, and the sides about these equal angles are proportional, the triangles are similar
6. The ratio of the areas of similar triangles is equal to the ratio of the squares on corresponding sides
7. The opposite sides of a parallelogram are equal: the opposite angles are equal; and a diagonal bisects the area of a parallelogram
8. The diagonals of a parallelogram bisect each other
9. If the opposite sides of a quadrilateral are equal, then the quadrilateral must be a parallelogram
10. If the opposite angles of a quadrilateral are equal, then the quadrilateral must be a parallelogram
11. If the diagonals of a quadrilateral bisect each other, then the quadrilateral must be a parallelogram
12. If one pair of opposite sides of a quadrilateral are equal and parallel, then the other sides must be equal and parallel and the quadrilateral must be a parallelogram
13. The line drawn through the mid-point of one side of a triangle parallel to a second side bisects the third side
14. The straight line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half of it
15. If there are three or more parallel straight lines and the intercepts made by them on any straight line that cuts them are equal, then the corresponding intercepts on any other straight line that cuts them are also equal.
16. The locus of a point which is equidistant from two intersecting straight lines consists of the pair of straight lines which bisect the angles between the two given lines
17. The locus of a point which is equidistant from two intersecting straight lines consists of the pair of straight lines which bisect the angles between the two given lines
18. Parallelograms on the same base and between the same parallels are equal in area
19. The area of a triangle is half that of a parallelogram drawn on the same base and between the same parallels
20. The theorem of Pythagoras -
The square on the hypotenuse of a right-angled triangle is equal to the sum of the squares on the other two sides
21. The converse of Pythagoras -
If the sum of the squares on two sides of a triangle is equal to the square on the third side, the angle opposite this third side must be a right angle
Chapter - 1
Ratio & Percentage
A ratio is used to compare two or more quantities of the same kind which are measured in the same unit.
A ratio is usually expressed as a fraction in its lowest terms.
Suppose we have two sticks, one 100 cm long and the other 60 cm long. If the first is divided into 5 equal parts, each part will be 20cm long. If the second is divided into 3 equal parts, each part will also be 20 cm long. The lengths of the two sticks are said to be "in the ratio 5 to 3". This is often written 'the lengths of the two sticks are in the ratio 5:3'.
1. A straight line drawn parallel to one side of a triangle divides the other sides in the same ratio.
The theorem holds even if the line XY meets the sides AB, AC produced. In both cases of the figure,
AX/XB = AY/YC.
Notice that the ratio of any two lengths on line AB is equal to the ratio of the corresponding lengths on AC.
The corresponding lengths are AB and AC; AX and AY; BX and CY.
For example, AX/AB = AY/AC and XB/AB = YC/AC
The converse of this theorem also applies.
Q.1. Construct ABC such that AB = 8 cm, BC = 6.5 cm, and BAC = 90. Measure and write down the length of AC.
Q.2. Construction of a Triangle Given 2 sides and an included Angle)
Construct ABC such that AB = 10.5 cm, BC = 7.5 cm and ABC = 60.
i) Measure and write down the length of AC.
ii) Construct the perpendicular bisector of AB such that it cuts AC.
Measure and write down the length of BS, such that S is the point where the perpendicular bisector of AB cuts AC.
Construction Steps:
1. Using a ruler, draw AB = 10.5 cm
2. Since B = 60, using a protractor at B, mark off an angle of 60 and draw a line BK such that ABK = 60.
3. Since C is 7.5 cm away from B, with B as centre and 7.5 cm as radius, draw an arc to cut BK at C.
4. Join AC.
5. Length of AC = 9.4 cm.
ii) Construction Steps:
1. With A as centre and radius more than half the length of AB, draw arc 1 above AB and draw arc 2 below AB.
2. With B as centre and radius the same as in the previous step, draw arc 3 to cut arc 1 at x and draw arc 4 to cut arc 2 Y.
3. Join XY to obtain the perpendicular bisector of AB.
4. Extend the perpendicular bisector of AB such that it cuts AC. Label the point where the perpendicular bisector of AB cuts AC as S.
Join BS using a dotted line.
Length of BS = 7.3 cm.
Basic level:
1. Draw a line segment AB of length 9.5 cm. Construct the perpendicular bisector of AB.
2. Draw an angle BAC of 56 degrees. Construct the angle bisector of BAC.
3. Construct ABC such that AB = 8 cm, BC = 6.5 cm and ABC = 80 degrees. Measure and write down the length of AC.
4. Construct ABC such that AB = 5 cm, BC = 9 cm and BAC = 90 degrees. Measure and write down the length of AC.
5. Construct an isosceles triangle PQR such that PQ = PR = 10 cm and QR = 9 cm. Measure and write down the size of QPR.
6. Construct an equilateral triangle with sides 9.5 cm each.
7. Construct XYZ such that XY = 10.2 cm, XYZ = 60 degrees and YXZ = 45 degree. Measure and write down the length of XZ.
2. If a straight line divides two sides of a triangle in the same ratio, then the line is parallel to the other side of the triangle.
If, in Fig. AX/XB = AY/YC, then XY is parallel to BC.
3. If two triangles are equiangular, their corresponding sides are proportional.
4. If two triangles have their corresponding sides proportional, they are equiangular.
If AB/XY = AC/XZ = BC/YZ, then the corresponding sides are
AB and XY; AC and XZ; BC and YZ.
The angles opposite corresponding sides are equal, i.e. angle A equals angle X, angle B equals angle Y and angle C equals angle Z.
Make a habit of writing the order of the letters in similar triangles so that equal angles correspond. For example, in figure say that the triangles
ABC and XYZ are similar but do not say that the triangles ACB and ZYX are similar.
5. If two triangles have one angle of the one equal to one angle of the other, and the sides about these equal angles are proportional, the triangles are similar.
6. The ratio of the areas of similar triangles is equal to the ratio of the squares on corresponding sides.
7. The opposite sides of a parallelogram are equal; the opposite angles are equal; and a diagonal bisects the area of a parallelogram.
If two pairs of parallel lines are drawn as in figure, they will form a quadrilateral which is called a parallelogram.
A parallelogram is a quadrilateral with its opposite sides parallel.
Properties:
From this definition of a parallelogram, it is possible to prove the following four properties. All are proved by congruent triangles by joining two opposite vertices of the parallelogram. A line joining two opposite vertices of a quadrilateral is called a diagonal.
a) Both pairs of opposite sides are equal.
b) A diagonal bisects the area of a parallelogram.
c) Both pairs of opposite angles are equal.
d) The diagonals bisect each other.
8. The diagonals of a parallelogram bisect each other.
9. If the opposite sides of a quadrilateral are equal, then the quadrilateral must be a parallelogram
10. If the opposite angles of a quadrilateral are equal, then the quadrilateral must be a parallelogram
11. If the diagonals of a quadrilateral bisect each other, then the quadrilateral must be a parallelogram
12. If one pair of opposite sides of a quadrilateral are equal and parallel, then the other sides must be equal and parallel and the quadrilateral must be a parallelogram.
13. The line drawn through the mid-point of one side of a triangle parallel to a second side bisects the third side.
14. The straight line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half of it.
15. If there are three or more parallel straight lines and the intercepts made by them on any straight line that cuts them are equal, then the corresponding intercepts on any other straight line that cuts them are also equal.
16. The locus of a point which is equidistant from two fixed points is the perpendicular bisector of the straight line joining the two fixed points.
17. The locus of a point which is equidistant from two intersecting straight lines consists of the pair of straight lines which bisect the angles between the two given lines.
18. Parallelograms on the same base and between the same parallels are equal in area.
19. The area of a triangle is half that of a parallelogram drawn on the same base and between the same parallels.
20. The theorem of Pythagoras: –
The square on the hypotenuse of a right–angled triangle is equal to the sum of the squares on the other two sides
21. The converse of Pythagoras: –
If the sum of the squares on two sides of a triangle is equal to the square on the third side, the angle opposite this third side must be a right angle.
Division of a straight line two parts of a given ratio:
Suppose AB is a straight line of length 5 cm and we wish to divide it into two parts in the ratio 3:7.
Let C be the point of division.
Suppose the length of AC is 3 units and the length of CB is 7 units. The length of AB must be 10 units which therefore equals 5 cm. Each unit is therefore 0.5 cm. The length of AC is hence 1.5 cm and that of CB 3.5 cm.
Division by Construction:
Through A draw any line AY and mark on it any 10 equal distances (3 + 7), AP< PQ, QR etc.
Suppose the tenth point marked is Y. Join YB.
Through R, the third point on the line AY, draw RC parallel to YB to meet AB at C. Then C divides AB in the ratio 3:7.
External division of a straight line:
Suppose XY is a straight line of length 8 cm and we wish to find a point Z on XY produced so that XY : YZ = 7:3.
Suppose the length of XZ is 7 units and that of YZ 3 units. Then the length of XY must be 7 units – 3 units or 4 units.
But the length of XY is given to be 8 cm. Therefore each unit must equal 2 cm and the length of XZ is 14 cm.
